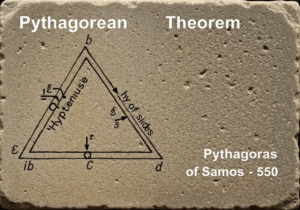
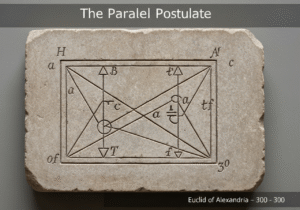
A fundamental theorem in Euclidean geometry states that the sum of the measures of the three interior angles of any triangle is always equal to two right angles, or 180 degrees. This property, \(\alpha + \beta + \gamma = 180^\circ\), is a direct consequence of the parallel postulate and holds true for all triangles, regardless of their size or shape, within a flat, Euclidean plane.