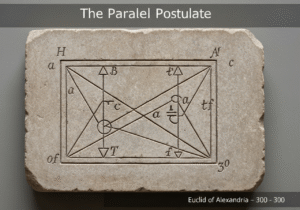
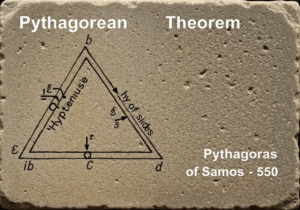
Also known as the method of indivisibles, this principle states that if two solids lying between two parallel planes have the property that every plane parallel to the two given planes intersects them in cross-sections of equal area, then the two solids have equal volumes. It provides a powerful method for calculating volumes of complex shapes without calculus.