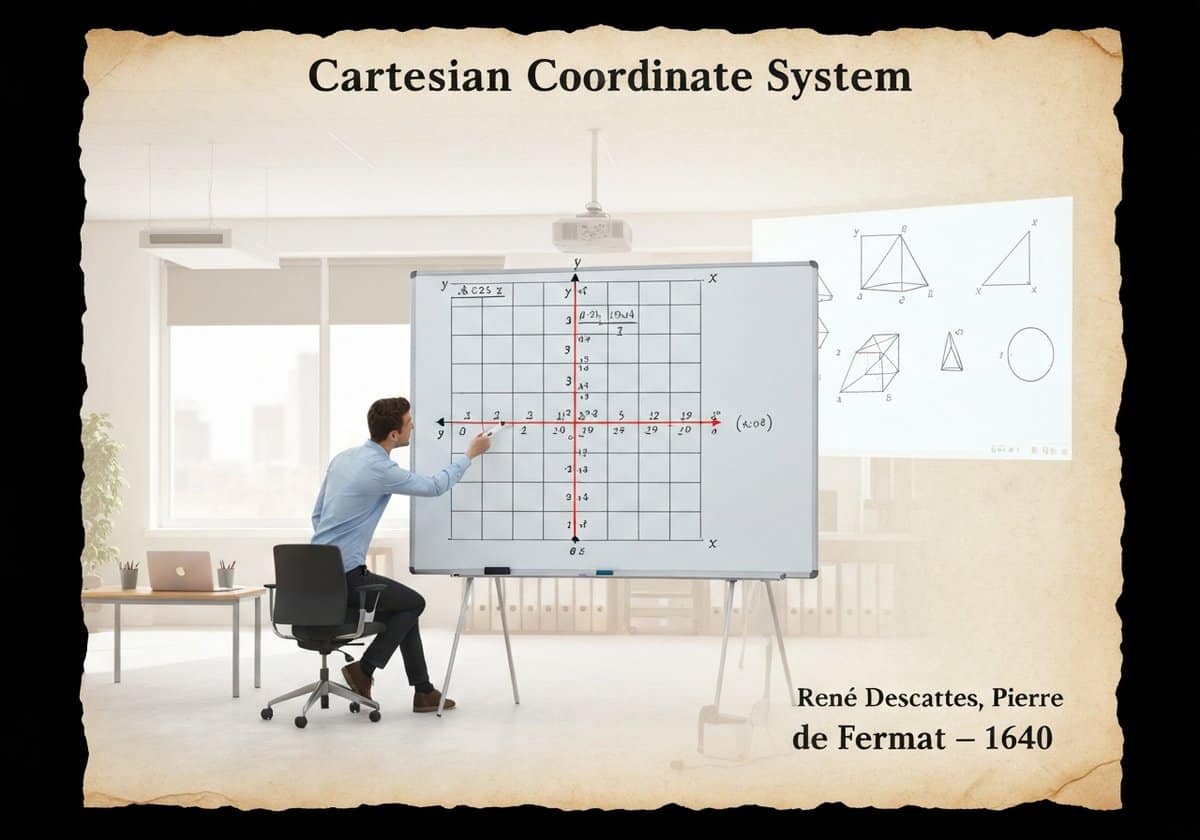
The Cartesian coordinate system provides an algebraic model for Euclidean geometry. It uses one or more numbers, or coordinates, to uniquely determine the position of a point in space. In a plane, two perpendicular lines (the x-axis and y-axis) are used, allowing geometric shapes to be described by algebraic equations. This fusion of algebra and geometry is known as analytic geometry.