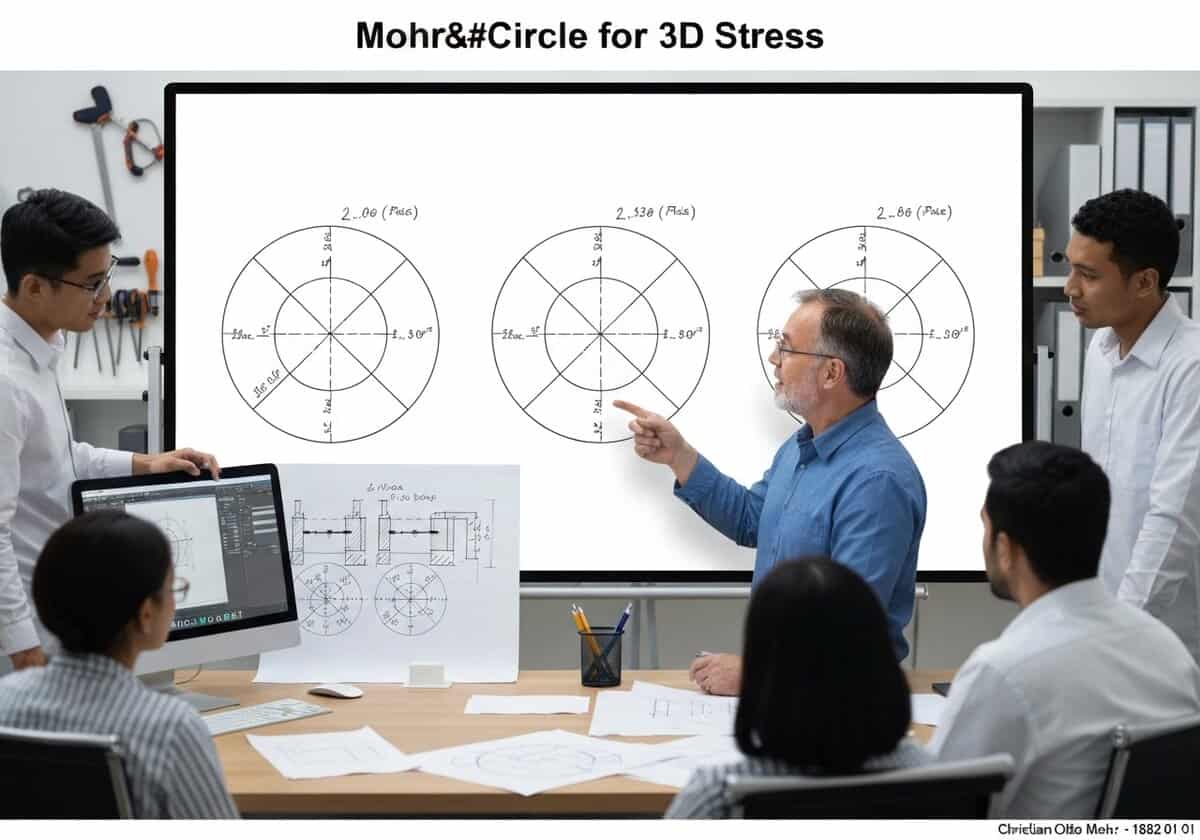
For a general three-dimensional state of stress, the analysis is represented by three Mohr’s circles. These circles are drawn in the [latex]\sigma_n – \tau_n[/latex] plane using the three principal stresses ([latex]\sigma_1, \sigma_2, \sigma_3[/latex]) as diameters. The largest circle, defined by [latex]\sigma_1[/latex] and [latex]\sigma_3[/latex], encloses the other two and determines the absolute maximum shear stress, [latex]\tau_{abs max} = (\sigma_1 – \sigma_3)/2[/latex].