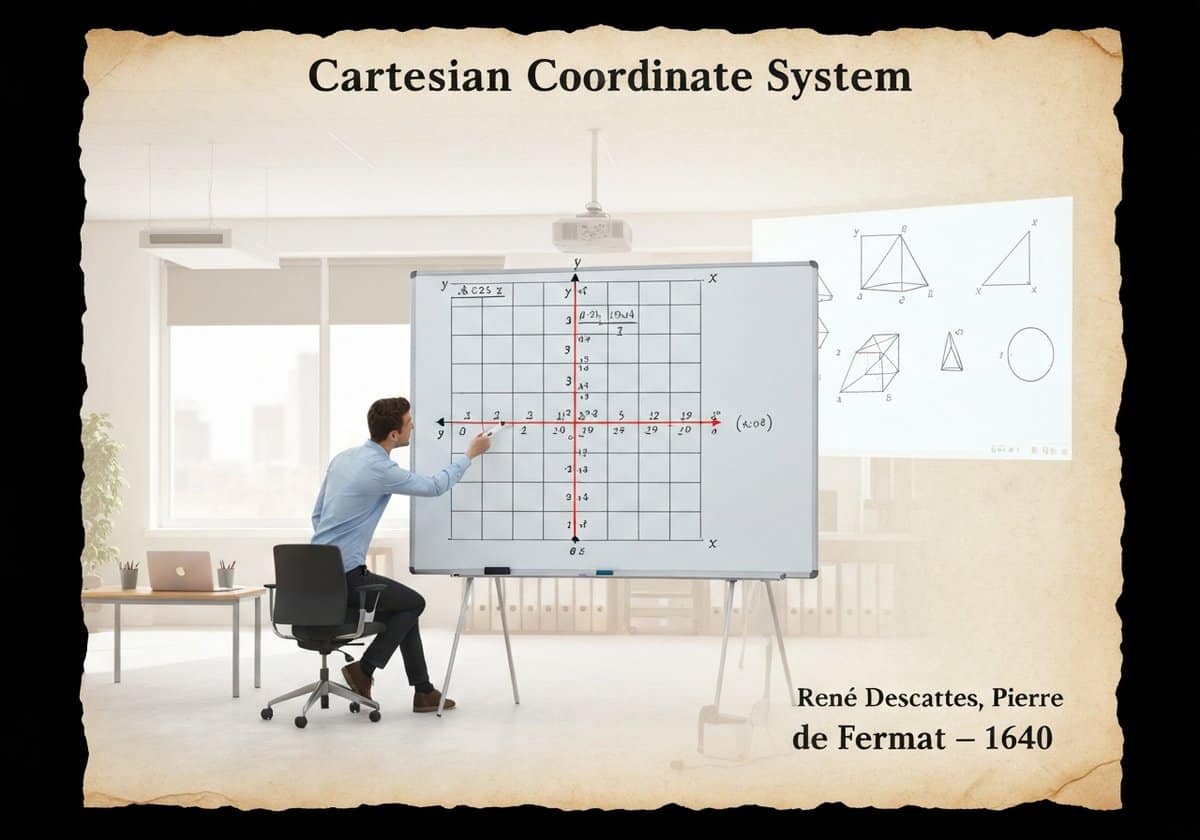
Le système de coordonnées cartésiennes fournit un modèle algébrique pour la géométrie euclidienne. Il utilise un ou plusieurs nombres, ou coordonnées, pour déterminer de manière unique la position d'un point dans l'espace. Dans un plan, deux droites perpendiculaires (l'axe des x et l'axe des y) sont utilisées, ce qui permet de décrire des formes géométriques par des équations algébriques. Cette fusion de l'algèbre et de la géométrie est appelée géométrie analytique.