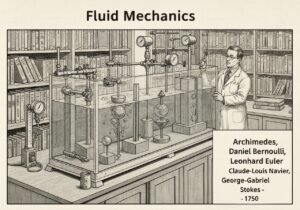
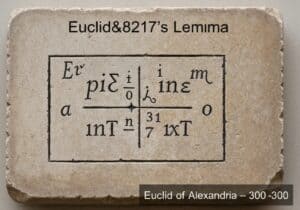
These are two ways to describe motion in continuum mechanics:
- IL Lagrangian specification follows individual material particles, tracking their properties over time, like watching a specific car in traffic
- La specifica euleriana si concentra sui punti fissi nello spazio, osservando le proprietà (velocità, densità) di qualsiasi particella passi attraverso quei punti, come una telecamera per il traffico che osserva un'intersezione fissa.