For a general three-dimensional state of stress, the analysis is represented by three Mohr’s circles. These circles are drawn in the [latex]\sigma_n – \tau_n[/latex] plane using the three principal stresses ([latex]\sigma_1, \sigma_2, \sigma_3[/latex]) as diameters. The largest circle, defined by [latex]\sigma_1[/latex] and [latex]\sigma_3[/latex], encloses the other two and determines the absolute maximum shear stress, [latex]\tau_{abs max} = (\sigma_1 – \sigma_3)/2[/latex].
Mohr’s Circle for 3D Stress
- Christian Otto Mohr
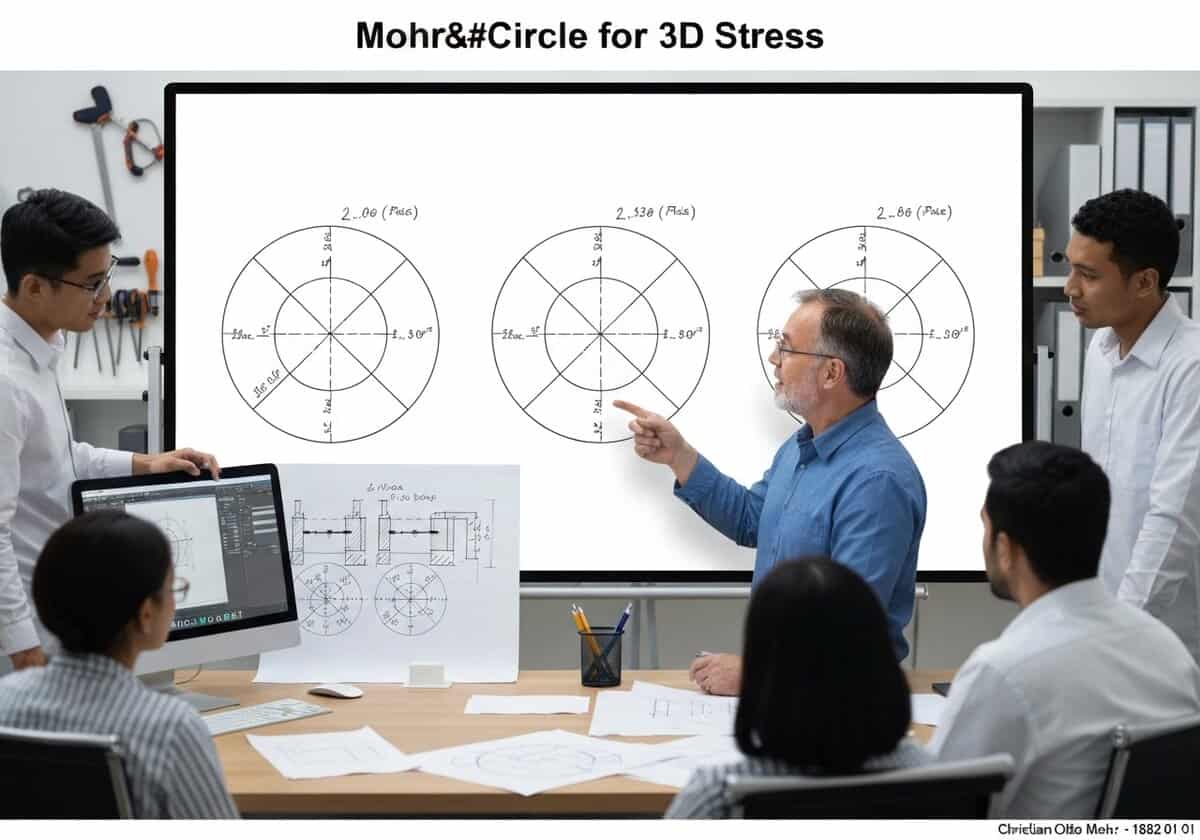
While the 2D Mohr’s circle is common, real-world stress states are three-dimensional. To analyze a 3D stress state, one first determines the three principal stresses, [latex]\sigma_1 \ge \sigma_2 \ge \sigma_3[/latex], which are the eigenvalues of the 3×3 Cauchy stress tensor. These three values are then used to construct three separate Mohr’s circles. The first circle is drawn between [latex]\sigma_1[/latex] and [latex]\sigma_2[/latex], the second between [latex]\sigma_2[/latex] and [latex]\sigma_3[/latex], and the third, largest circle between [latex]\sigma_1[/latex] and [latex]\sigma_3[/latex].
The stress state ([latex]\sigma_n, \tau_n[/latex]) for any arbitrarily oriented plane at the point will lie within the shaded area bounded by these three circles. A crucial insight from this 3D representation is the determination of the absolute maximum shear stress. Unlike the 2D case where the maximum in-plane shear is the radius, the absolute maximum shear stress for a 3D state is always the radius of the largest circle, given by [latex]\tau_{abs max} = R_{max} = (\sigma_{max} – \sigma_{min})/2 = (\sigma_1 – \sigma_3)/2[/latex]. This value is fundamental for applying failure criteria like the Tresca yield criterion in a general 3D context, as it represents the true maximum shear stress experienced by the material at that point.
Taper
Perturbation
Usage
Précurseurs
- Cauchy’s 3D stress tensor formulation
- Eigenvalue analysis for 3×3 matrices
- Mohr’s original 2D circle concept
- Lamé’s stress ellipsoid concept
Applications
Brevets:
Idées d'innovations potentielles
!niveaux !!! Adhésion obligatoire
Vous devez être membre de l'association pour accéder à ce contenu.
DISPONIBLE POUR DE NOUVEAUX DÉFIS
Ingénieur mécanique, chef de projet, ingénierie des procédés ou R&D
Disponible pour un nouveau défi dans un court délai.
Contactez-moi sur LinkedIn
Intégration électronique métal-plastique, Conception à coût réduit, BPF, Ergonomie, Appareils et consommables de volume moyen à élevé, Production allégée, Secteurs réglementés, CE et FDA, CAO, Solidworks, Lean Sigma Black Belt, ISO 13485 médical
Nous recherchons un nouveau sponsor
Votre entreprise ou institution est dans le domaine de la technique, de la science ou de la recherche ?
> envoyez-nous un message <
Recevez tous les nouveaux articles
Gratuit, pas de spam, email non distribué ni revendu
ou vous pouvez obtenir votre adhésion complète - gratuitement - pour accéder à tout le contenu restreint >ici<
Contexte historique
Mohr’s Circle for 3D Stress
(si la date est inconnue ou non pertinente, par exemple « mécanique des fluides », une estimation arrondie de son émergence notable est fournie)
Inventions, innovations et principes techniques connexes