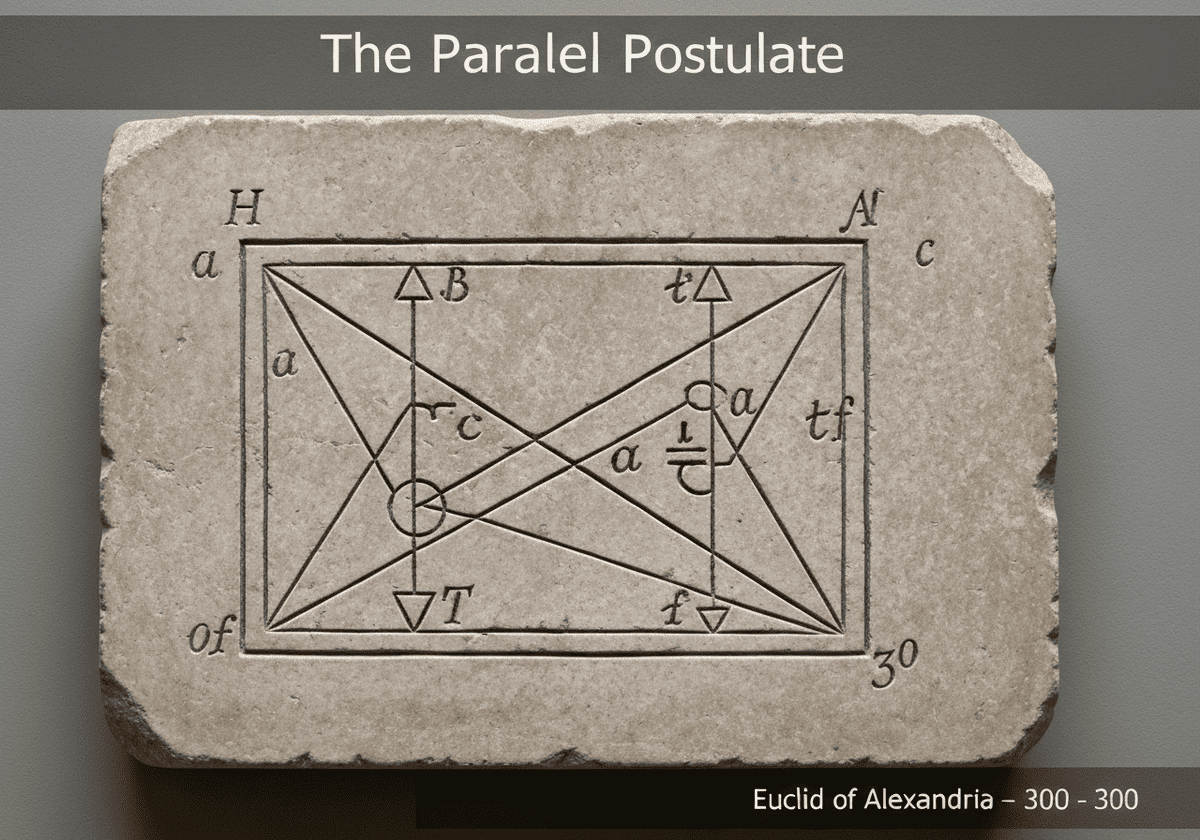
Euclid’s fifth postulate, the parallel postulate, is the axiom that defines Euclidean geometry: it states that if a line intersects two other lines, and the interior angles on one side sum to less than two right angles ([latex]\alpha + \beta < 180^\circ[/latex]), then the two lines will eventually intersect on that side. This postulate guarantees a unique parallel line through a point not on a given line.