Mohr’s circle is a two-dimensional graphical representation of the Cauchy stress tensor. It visualizes the transformation of normal stress ([latex]\sigma_n[/latex]) and shear stress ([latex]\tau_n[/latex]) on an arbitrarily oriented plane at a point. The abscissa of each point on the circle is the normal stress, and the ordinate is the shear stress, allowing for easy determination of principal stresses.
Mohr’s Circle for Stress
- Christian Otto Mohr
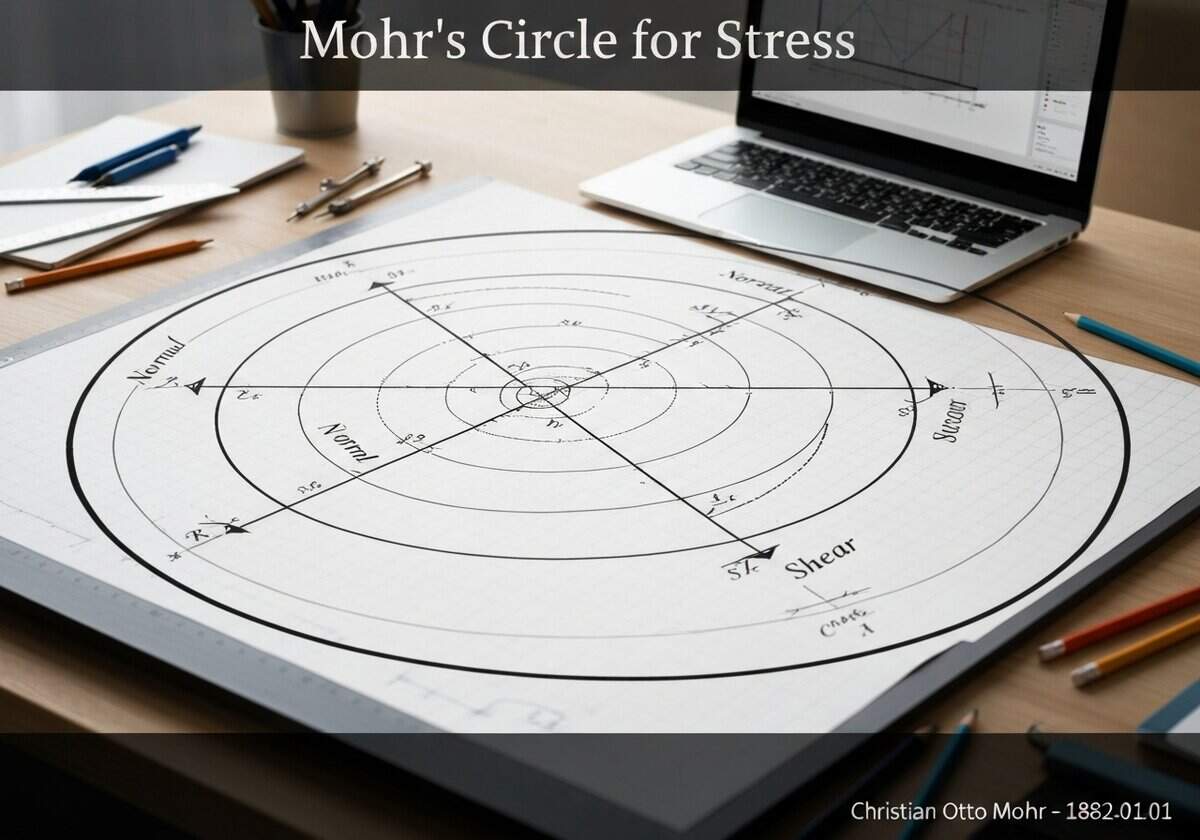
Mohr’s circle provides a powerful graphical tool to understand the state of Stress at a point within a continuous body. For any given 2D stress state defined by normal stresses [latex]\sigma_x[/latex], [latex]\sigma_y[/latex] and shear stress [latex]\tau_{xy}[/latex], the circle allows one to find the stresses on any plane passing through that point. The center of the circle is located on the [latex]\sigma_n[/latex] axis at [latex]C = (\sigma_{avg}, 0)[/latex], where [latex]\sigma_{avg} = (\sigma_x + \sigma_y)/2[/latex]. The radius of the circle is calculated as [latex]R = \sqrt{\left(\frac{\sigma_x – \sigma_y}{2}\right)^2 + \tau_{xy}^2}[/latex]. Each point on the circumference of the circle represents the stress state ([latex]\sigma_n, \tau_n[/latex]) on a specific plane. A rotation of an angle [latex]\theta[/latex] of the physical plane corresponds to a rotation of [latex]2\theta[/latex] on Mohr’s circle in the same direction. This graphical Verfahren elegantly bypasses the need to solve the stress transformation equations directly for each angle, making it an intuitive and efficient method for engineers and physicists.
Historically, Christian Otto Mohr developed this method in 1882. It was a significant advancement over purely analytical methods, providing a visual aid that greatly simplified the complex mathematics of stress transformation. Before Mohr, engineers relied on Augustin-Louis Cauchy’s stress tensor formulation, which was powerful but less intuitive for practical design applications. Mohr’s graphical approach made the concepts of principal stresses and maximum shear stress accessible, which are fundamental to predicting material failure according to theories like Tresca’s or von Mises’ criteria.
Typ
Unterbrechung
Verwendung
Vorläufersubstanzen
- Cauchy’s stress tensor theory
- Principles of stress transformation equations
- Coordinate geometry and the equation of a circle
- Euler’s work on principal axes of inertia
Anwendungen
- structural engineering for designing beams and columns
- geotechnical engineering for analyzing soil and rock stability
- mechanical engineering for designing machine components under load
- materials science for studying failure criteria
Patente:
Mögliche Innovationsideen
!Professionals (100% free) Mitgliedschaft erforderlich
Sie müssen ein Professionals (100% free) Mitglied sein, um auf diesen Inhalt zugreifen zu können.
VERFÜGBAR FÜR NEUE HERAUSFORDERUNGEN
Maschinenbauingenieur, Projekt-, Verfahrenstechnik- oder F&E-Manager
Kurzfristig für eine neue Herausforderung verfügbar.
Kontaktieren Sie mich auf LinkedIn
Integration von Kunststoff-Metall-Elektronik, Design-to-Cost, GMP, Ergonomie, Geräte und Verbrauchsmaterialien in mittleren bis hohen Stückzahlen, Lean Manufacturing, regulierte Branchen, CE und FDA, CAD, Solidworks, Lean Sigma Black Belt, medizinische ISO 13485
Wir suchen einen neuen Sponsor
Ihr Unternehmen oder Ihre Institution beschäftigt sich mit Technik, Wissenschaft oder Forschung?
> Senden Sie uns eine Nachricht <
Erhalten Sie alle neuen Artikel
Kostenlos, kein Spam, E-Mail wird nicht verteilt oder weiterverkauft
oder Sie können eine kostenlose Vollmitgliedschaft erwerben, um auf alle eingeschränkten Inhalte zuzugreifen >Hier<
Historischer Kontext
Mohr’s Circle for Stress
(wenn das Datum nicht bekannt oder nicht relevant ist, z. B. "Strömungsmechanik", wird eine gerundete Schätzung des bemerkenswerten Erscheinens angegeben)
Verwandte Erfindungen, Innovationen und technische Prinzipien