家 » Mohr’s Circle for Stress

Mohr’s Circle for Stress

1882-01-01

Christian Otto Mohr

Mohr’s circle is a two-dimensional graphical representation of the Cauchy stress tensor. It visualizes the transformation of normal stress ([latex]\sigma_n[/latex]) and shear stress ([latex]\tau_n[/latex]) on an arbitrarily oriented plane at a point. The abscissa of each point on the circle is the normal stress, and the ordinate is the shear stress, allowing for easy determination of principal stresses.

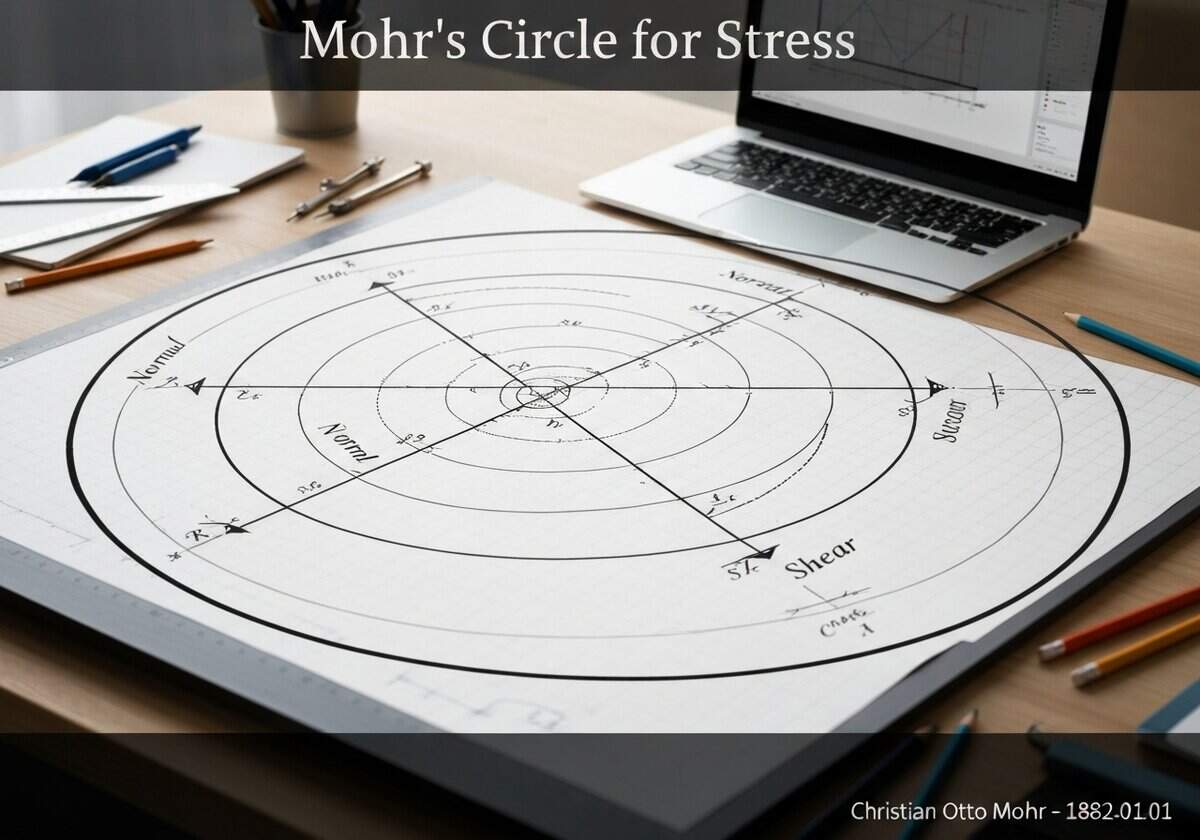
Mohr’s circle provides a powerful graphical tool to understand the state of 强调 at a point within a continuous body. For any given 2D stress state defined by normal stresses [latex]\sigma_x[/latex], [latex]\sigma_y[/latex] and shear stress [latex]\tau_{xy}[/latex], the circle allows one to find the stresses on any plane passing through that point. The center of the circle is located on the [latex]\sigma_n[/latex] axis at [latex]C = (\sigma_{avg}, 0)[/latex], where [latex]\sigma_{avg} = (\sigma_x + \sigma_y)/2[/latex]. The radius of the circle is calculated as [latex]R = \sqrt{\left(\frac{\sigma_x – \sigma_y}{2}\right)^2 + \tau_{xy}^2}[/latex]. Each point on the circumference of the circle represents the stress state ([latex]\sigma_n, \tau_n[/latex]) on a specific plane. A rotation of an angle [latex]\theta[/latex] of the physical plane corresponds to a rotation of [latex]2\theta[/latex] on Mohr’s circle in the same direction. This graphical 方法 elegantly bypasses the need to solve the stress transformation equations directly for each angle, making it an intuitive and efficient method for engineers and physicists.

Historically, Christian Otto Mohr developed this method in 1882. It was a significant advancement over purely analytical methods, providing a visual aid that greatly simplified the complex mathematics of stress transformation. Before Mohr, engineers relied on Augustin-Louis Cauchy’s stress tensor formulation, which was powerful but less intuitive for practical design applications. Mohr’s graphical approach made the concepts of principal stresses and maximum shear stress accessible, which are fundamental to predicting material failure according to theories like Tresca’s or von Mises’ criteria.

面向制造设计 (DfM), 可靠性设计（DfR）, 设计思维, 有限元法（FEM）, 材料科学, 机械工业, 机械, 应力腐蚀, 结构工程

UNESCO Nomenclature: 2203

– Classical mechanics

类型

抽象系统

中断

实质性

使用方法

广泛使用

前体

Cauchy’s stress tensor theory
Principles of stress transformation equations
Coordinate geometry and the equation of a circle
Euler’s work on principal axes of inertia

应用

structural engineering for designing beams and columns
geotechnical engineering for analyzing soil and rock stability
mechanical engineering for designing machine components under load
materials science for studying failure criteria

专利：

潜在的创新想法

级别需要会员

您必须是！！等级！！会员才能访问此内容。

立即加入

已经是会员？在此登录

Related to: Mohr’s circle, stress analysis, continuum 力学, graphical method, principal stress, shear stress, Cauchy stress tensor, solid mechanics, structural engineering, geotechnical engineering.