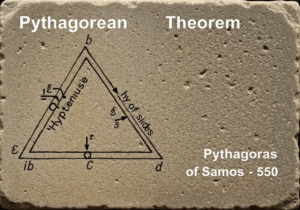
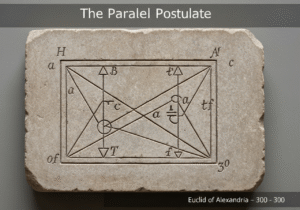
Un teorema fondamentale della geometria euclidea afferma che la somma delle misure dei tre angoli interni di qualsiasi triangolo è sempre uguale a due angoli retti, o a 180 gradi. Questa proprietà, [latex]\alfa + \beta + \gamma = 180^circ[/latex], è una conseguenza diretta del postulato delle parallele e vale per tutti i triangoli, indipendentemente dalla loro dimensione o forma, all'interno di un piano euclideo.