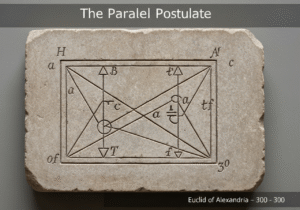
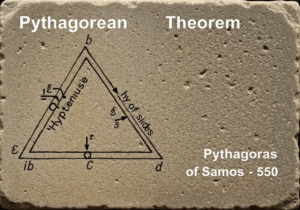
Si tratta di un problema storicamente notevole in matematica. La sua risoluzione negativa da parte di Leonhard Euler nel 1736 ha posto le basi della teoria dei grafi e ha prefigurato l'idea di topologia. Il problema chiedeva se i sette ponti della città di Königsberg potessero essere attraversati tutti in un solo viaggio senza tornare indietro, e se il viaggio terminasse sulla stessa terraferma da cui era partito.