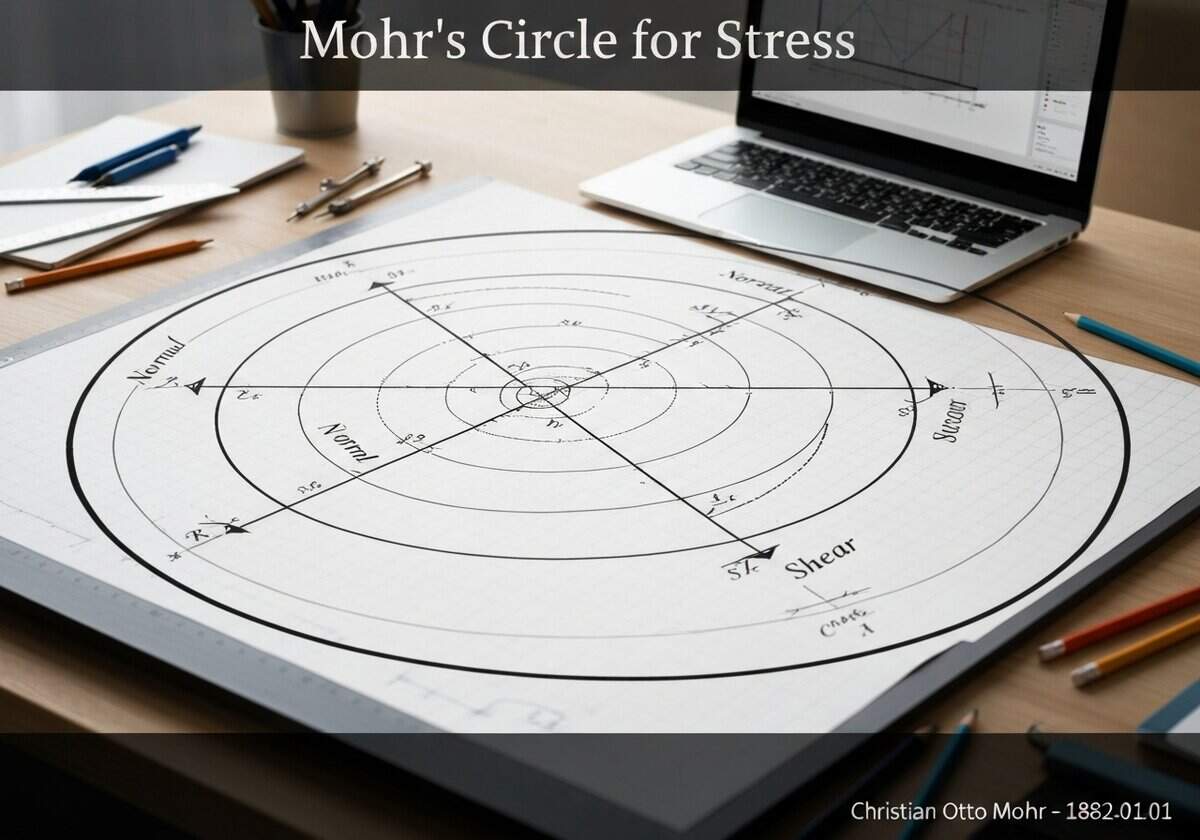
Mohr’s circle is a two-dimensional graphical representation of the Cauchy stress tensor. It visualizes the transformation of normal stress ([latex]\sigma_n[/latex]) and shear stress ([latex]\tau_n[/latex]) on an arbitrarily oriented plane at a point. The abscissa of each point on the circle is the normal stress, and the ordinate is the shear stress, allowing for easy determination of principal stresses.