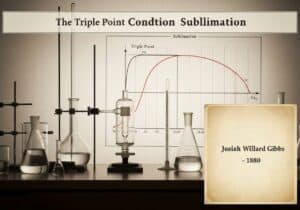
This foundational formula connects the macroscopic termodinámica quantity of entropy (S) with the number of possible microscopic arrangements, or microstates (W), corresponding to the system’s macroscopic state. The equation, [latex]S = k_B \ln W[/latex], reveals that entropy is a measure of statistical disorder or randomness. The constant [latex]k_B[/latex] is the Boltzmann constant, linking energy at the particle level with temperature.