مكعب روبيك: الخطوات الأساسية الـ 15 لحلها

ليس فقط للمهندسين(مبتذل!): تعلم حل مكعب روبيك في أقل من ساعتين. نادراً ما استمرت أي أحجية لفترة طويلة. فبعد مرور ما يقرب من خمسين عامًا على اختراعه، لا يزال مكعب روبيك© يحتفظ باهتمام الجيل التالي به، حيث يتم تطوير أشكاله المختلفة بحيث تكون الابتكارات التقنية. من المكعبات المجتمعات مع 100 من القنوات المخصصة على الإنترنت والمطبوعات و سبيدكابينج المسابقات، فإن شعبية هذا اللغز لا مثيل لها.

اخترع المهندس المعماري المجري إرنو روبيك© مكعب روبيك الذي سُمّي في البداية بالمكعب السحري، وقد اخترعه المهندس المعماري المجري إرنو روبيك في عام 1974، وأُنتج لأول مرة في عام 1977، وحقق نجاحاً عالمياً في الثمانينيات.

وبعد مرور ثلاثين عامًا، تم إنتاج ما لا يقل عن 350 مليون مكعب حتى براءة الاختراع انتهت صلاحيتها وتم إنتاج المزيد من الملايين منها منذ ذلك الحين.

نحن نعتقد اعتقاداً راسخاً أن النجاح الكبير الذي حققه مكعب روبيك يرجع أساساً إلى على ما يبدو عدد مذهل من التركيبات ("يجب أن تكون جائزة نوبل لحل هذه المشكلة!") ومع ذلك مع تصميم بسيطوبسيط مبدأ اللون ... ولكنها في الواقع ممكنة في وقت أقل من العديد من الألغاز ثنائية الأبعاد.

تناول القهوة، وتصفح الصفحة مع الفيديو,
وخلال ساعتين يكون المكعب لك!

حل مكعب روبيك

على مر العقود، تم تطوير العديد من الاستراتيجيات المنطقية (انظر رابط ويكيبيديا أدناه) مع تسلسلها الخاص لحل المكعب بتات بتات. تنطوي الطرق المختلفة على تسلسلات أكثر أو أقل تعقيداً لتعلمها. نقترح هنا تعلم أبسط طريقة، تتكون من حل المكعب طبقة تلو الأخرى, مع التسلسلات غير المحسّنة و الحفاظ على ما تم وضعه من قبل. لمعلوماتك، في العديد من طرق تحطيم الأرقام القياسية، أو الطريقة المحوسبة المشار إليها في أسفل هذا المنشور، لا ترى القطع الموضوعة في موضعها النهائي حتى الحركات الأخيرة، مما يجعل من الصعب جدًا رؤية التقدم الصحيح.

باتباع الخطوات ومقطع الفيديو أدناه، يستغرق تعلم كيفية حل مكعب روبيك© حوالي ساعتين في غضون 5 دقائق

أفضل فيديو تعليمي لتعلم الأنواع الثلاثة من القطع، والحركات الأساسية، والتركيبات الأولى (الطريقة معروفة وشائعة في العديد من الكتب والمواقع، ولكنها بالتأكيد واضحة وشاملة للغاية هنا من خلال ذا كوبيكل):

[embedyt] https://www.youtube.com/watch?v=1t1OL2zN0LQ[/embedyt]

سيتم استخدام تسلسلين أساسيين بشكل متكرر خلال الطريقة. نوصي بممارسة هذه 2 أولاًحتى لا تفسد المكعب في منتصف الحل وتضطر إلى البدء من الصفر مرة أخرى (كما فعلنا جميعًا!). تجدر الإشارة إلى أنه إذا كررت أيًا منها 6 مرات متتالية، يعود المكعب إلى حالته الأصلية:

"يمين ALG" = R U R' U' U'

"اليسار ALG" = L' U' L' L' U

ملاحظة: تدور اليد الرئيسية وتتحرك الأصابع ولكن إذا كانت الوضعية الأولية صحيحة، فلا تحتاج إلى إعادة وضعها بين الخطوات، مما يجعل هاتين المتتابعتين سريعتين للغاية.

مساعدة! يمكن للمرء أيضًا إدخال أي مجموعة في هذه اللطيفة محاكي مكعب روبيك ثلاثي الأبعاد على الإنترنت لتصور أي تسلسل، مثل التسلسلين أعلاه

حل الطبقة السفلية

• اصنع الصليب الأبيض
  • أولاً، ضع البتلات الأربع حول المركز الأصفر: ابحث بنفسك عن الحركات الأساسية من 1 إلى 3 لوضع كل بتلة من البتلات الأربع البيضاء :)
  • ثم اعكس التقاطع: جانب بعد جانب: قم بمحاذاة لون وسط الطبقة الثانية المطابق للون الموجود على نفس الجانب ولكن على الطبقة العلوية. عندها فقط اقلب ذلك الجانب الكامل 180 درجة. بمجرد الانتهاء من ذلك على الجوانب الأربعة، يجب أن يكون لديك صليب أبيض كامل على الوجه السفلي مع وجود قطعتين متحاذيتين بنفس اللون على كل جانب.

• حلّ الزوايا الأربع البيضاء السفلية الأربع السفلية: ضع المكعب بحيث يكون الصليب الأبيض على الجانب السفلي. لكل زاوية ليست بيضاء بالفعل، ضع القطعة المطلوبة على الطبقة الأولى، فوق الموضع النهائي المطلوب. ثم كرر يمين ALG حتى يصل الجزء إلى الموضع الصحيح المطلوب. كرر لكل 3 زوايا إذا لم تكن بيضاء بالفعل.

حل الطبقة الوسطى

مع الخطوة السابقة، تكون جميع القطع المركزية الجانبية الأربعة في الموضع النهائي بالفعل. قد تكون حوافها الأربعة فقط غير صحيحة.

حل حواف الطبقة الوسطى الأربعة: لكل حافة تحتاج إلى الانضمام إلى الطبقة الوسطى (يعني عدم وجود حافة ذات جانب أصفر):

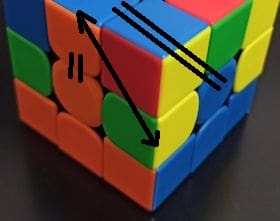
•  اقلب الطبقة العلوية وضع الحافة العلوية المرغوبة للتحرك فوق القطعة المركزية المجاورة من نفس اللون (مهم لأن هذا اللون سيبقى على نفس الوجه بعد الحركة فيما بعد)
• ثم يحتاج إلى الانضمام إلى موضعه الجانبي النهائي على الطبقة الوسطى إما بتحريكه إلى يسار أو يمين الطبقة الوسطى:
  • إذا إلى الحافة اليمنى: U, يمين ALGأدر المكعب إلى اليسار, أعسر ALG
  • إذا إلى الحافة اليسرى: U', أعسر ALGأدر المكعب إلى اليمين, Rأتي ALG

مع هذه الطبقة الثانية، يجب أن تكون الطبقتان السفليتان قد انتهيت من الطبقتين السفليتين بالكامل

حل الطبقة العليا، الوجه الأصفر

اجعل الصليب الأصفر على الوجه العلوي (انس أمر الزوايا في الوقت الحالي). الحالات الـ 3 المحتملة

• • إذا كان الخط المتقاطع فقط مكونًا بالفعل: وجِّه المكعب بحيث يكون الخط أفقيًا من اليسار إلى اليمين على الوجه العلوي، ثم

F, يمين ALG, F' ("F" هو دوران في اتجاه عقارب الساعة لـ 1 الوجه المواجه لك. F' عكس اتجاه عقارب الساعة)

• • إذا تم تشكيل زاوية واحدة فقط من التقاطع بالفعل: قم بتوجيه المكعب بحيث يكون هذا التقاطع الجزئي في أسفل يمين السطح العلوي، ثم قم بتطبيقه:

f, يمين ALG, f' ("f" هو دوران في اتجاه عقارب الساعة لـ 2 الطبقات الأمامية في مواجهتك. و'' عكس اتجاه عقارب الساعة)

• • إذا كان مركز الصليب الأصفر فقط قد تم تشكيله بالفعل: طبّق الخطوة الأولى أعلاه وستحصل على زاوية الصليب، ثم طبّق الخطوة الثانية للحصول على الصليب الأصفر الكامل

ضع 4 زوايا 4 زوايا (لكن الاتجاه الخاطئ/التحريف الخاطئ لا بأس به)

قم بتدوير الطبقة العلوية بحيث تكون الزوايا القصوى في موضعها النهائي (على سبيل المثال الزاوية الحمراء/الأخضر/الأصفر على