家 » 卡瓦列里原理

卡瓦列里原理

1635

Bonaventura Cavalieri

(generate image for illustration only)

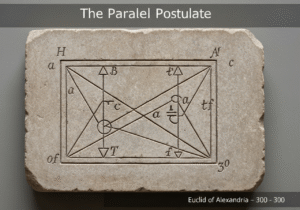
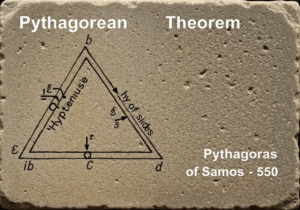
Also known as the 方法 of indivisibles, this principle states that if two solids lying between two parallel planes have the property that every plane parallel to the two given planes intersects them in cross-sections of equal area, then the two solids have equal volumes. It provides a powerful method for calculating volumes of complex shapes without calculus.

Cavalieri’s principle offers an elegant and intuitive way to determine the volume of three-dimensional objects. It formalizes the idea of slicing a solid into an infinite number of infinitesimally thin cross-sections, or “indivisibles.” The core idea is that if you have two solids, and for every possible height, the cross-sectional area of the first solid is equal to the cross-sectional area of the second solid, then their total volumes must be the same. It’s like comparing two stacks of coins; if each coin in one stack has the same area as the corresponding coin in the other stack, the total volume of metal is the same, regardless of how the stacks are skewed or arranged.

A classic application of this principle is to find the volume of a sphere. Consider a hemisphere of radius [latex]r[/latex]. Its cross-sectional area at a height [latex]h[/latex] from the base is a circle with area [latex]A = \pi(r’)^2[/latex]. By the Pythagorean theorem, [latex]h^2 + (r’)^2 = r^2[/latex], so [latex](r’)^2 = r^2 – h^2[/latex]. Thus, the area is [latex]A = \pi(r^2 – h^2)[/latex]. Now, consider a cylinder of radius [latex]r[/latex] and height [latex]r[/latex], with an inverted cone of the same radius and height removed from its center. The cross-sectional area of this shape at height [latex]h[/latex] is the area of the larger circle (from the cylinder) minus the area of the smaller circle (from the cone). This gives [latex]A = \pi r^2 – \pi h^2 = \pi(r^2 – h^2)[/latex].

Since the cross-sectional areas are identical at every height [latex]h[/latex], Cavalieri’s principle states that the volume of the hemisphere is equal to the volume of the cylinder-minus-cone shape. The volume of the cylinder is [latex]\pi r^2 \cdot r = \pi r^3[/latex], and the volume of the cone is [latex]\frac{1}{3}\pi r^2 \cdot r = \frac{1}{3}\pi r^3[/latex]. Therefore, the hemisphere’s volume is [latex]\pi r^3 – \frac{1}{3}\pi r^3 = \frac{2}{3}\pi r^3[/latex]. The volume of the full sphere is twice this, or [latex]\frac{4}{3}\pi r^3[/latex]. This method, developed by Bonaventura Cavalieri in the 17th century, was a significant step towards the development of integral calculus by Newton and Leibniz.

增材制造设计（DfAM）, 工程, 几何尺寸和公差, 几何学, 岩土工程, 数学

UNESCO Nomenclature: 1204

- 几何学

类型

抽象系统

中断

实质性

使用方法

广泛使用

前体

Archimedes’ method of exhaustion
Work of Zu Gengzhi in 5th-century China on calculating the volume of a sphere
The concept of infinitesimals in early mathematics

应用

calculating the volume of a sphere
deriving the volume formula for cones and pyramids
integral calculus (as a precursor concept)
computer tomography (ct) scan analysis for volume measurement
geotechnical engineering for estimating earthwork volumes

专利：

潜在的创新想法

级别需要会员

您必须是！！等级！！会员才能访问此内容。

立即加入

已经是会员？在此登录

Related to: cavalieri’s principle, method of indivisibles, volume calculation, integral calculus, cross-section, sphere volume, solid geometry, cylinder.