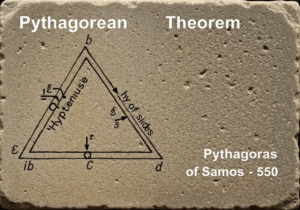
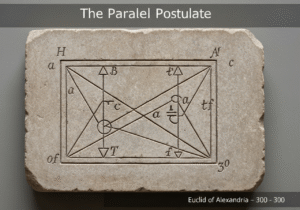
Euclid’s five postulates form the axiomatic basis for Euclidean geometry as described in his treatise, ‘Elements’. They are fundamental assumptions from which all other theorems are logically derived. The first four concern the construction of lines and circles, while the fifth, the parallel postulate, uniquely defines the flat, non-curved nature of Euclidean space. These axioms established the deductive 方法 in mathematics.